1283-C, *1500

Problem - C - Codeforces

문제

• $n(2\leq n \leq 2\cdot 10^{5})$명의 사람을 차례대로 1, 2, 3, ... , n 이라고 하자
• 각각의 사람이 누구에게 선물을 주어졌는지 주어진다. 이때 0 은 아직 선물을 주지 않은 사람이다
• 선물을 아직 주지 않은 사람은 다음 조건을 만족하도록 선물을 주어야한다
  1. 자기 자신에게는 주지 않는다
  2. 모든 사람은 선물을 적어도 하나 받는다
• 위 조건을 만족하도록 선물을 주는 경우를 아무거나 출력하라

 

$O(n)$

각각의 사람을 node, 선물을 주는 것을 edge 로 표현하여 위 문제를 graph 로 이해하자

그러면, 위 문제는 다음 조건을 만족시켜야 한다
1. 각각의 노드에서 뻗어나가는 edge 는 유일하게 존재한다
2. 각각의 노드는 오직 하나의 cycle 에 속한다
3. self cycle 은 허용되지 않는다

 

Claim
n-permutation of n 을 다음과 같이 해석하자. $a_{i}, i =1,\ 2,\ ...$는 i 번째 수를 의미한다
n개의 노드에 대해, node i 에서 node $a_{i}$로 가는 edge가 존재한다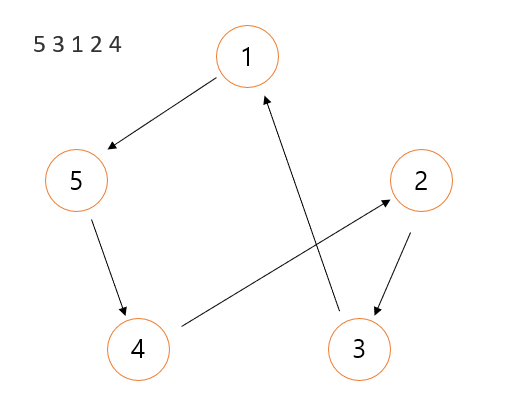

그러면 다음이 성립한다
i) 각각의 노드에서 뻗어나가는 edge 는 유일하게 존재한다
ii) 각각의 노드는 오직 하나의 cycle 에 속한다

$pf$ 
(i) trivial

(ii)
먼저 각각의 노드는 어떤 cycle 에 속함을 보이자.
순열에서는 1부터 n 까지의 수가 오직 한번만 등장한다 --- !

어떤 노드 i 에 대해
가. $a_{i} = i \Rightarrow$ self-cycle
나. $a_{i} = j(i \neq j)$ 일때
$a_{j} \neq j$($\because$ !)
$a_{a_{j}} \neq a_{j}$($\because$ !)
$a_{a_{a_{j}}} \neq a_{a_{j}}$($\because$ !)
...
이와 같은 과정을 반복하면
$a_{...a_{a_{j}}} = i$ 즉, i 는 어떤 cycle 에 속한다

한편, (i) 에 의해 i 가 속하는 사이클은 유일하다□

Claim 에 의해 $a_{i} = i$인 i 가 없는 permutation 은 문제의 조건을 만족시킨다
이를 문제의 상황과 연결지으면 0 인 부분에 1부터 n 중 등장하지 않은 숫자를 넣은 후
$a_{i} = i$ 인 것들만 자리를 바꿔주면 되겠다
ex)
5 0 0 2 4 ~ 1과 3이 없음
5 1 3 2 4 ~ $a_{3} = 3$ 이므로 자리바꿈
5 3 1 2 4 ~ 완성

7 0 0 1 4 0 6 ~ 2, 3, 5이 없음
7 2 3 1 4 5 6 ~ $a_{2} = 2$ 이므로 자리바꿈
7 3 2 1 4 5 6 ~ 완성

c++

#include <bits/stdc++.h>
#define endl "\n"
#define ooop(i, n) for(int i = 0; i < n; i++)
#define loop(i, n) for(int i = 1; i <= n; i++)
 
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
 
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
 
    int n;
    cin >> n;
    vector<int> cor(n), isreceived(n);
    vector<int> not_received, not_give;
    ooop(i, n){
        cin >> cor[i];
        cor[i]--;
        if(cor[i] == -1) not_give.emplace_back(i);
        else isreceived[cor[i]]++;
    }
 
    ooop(i, n){
        if(isreceived[i] == 0) not_received.emplace_back(i);
    }
 
    int k = not_give.size();
    ooop(i, k){
        cor[not_give[i]] = not_received[i];
    }
 
    ooop(i, k){
        if(cor[not_give[i]] == not_give[i]) swap(cor[not_give[i]], cor[not_give[(i+1)%k]]);
    }
 
    for(auto e: cor) cout << e+1 << ' ';
 
    return 0;
}cs

 

python 3

import sys
 
n = int(input())
cor = list(map(lambda x: x-1, map(int, sys.stdin.readline().split())))
not_give = [i for i, v in enumerate(cor) if v == -1]
 
isreceived = [0]*n
for i in cor:
    if i != -1: isreceived[i] = 1
not_received = [i for i, v in enumerate(isreceived) if v == 0]
 
k = len(not_give)
for i in range(k): cor[not_give[i]] = not_received[i]
 
for i in range(k):
    if(cor[not_give[i]]) == not_give[i]:
        cor[not_give[i]], cor[not_give[(i+1)%k]] = cor[not_give[(i+1)%k]], cor[not_give[i]]
 
print(*map(lambda x: x+1, cor))cs

 

참고

yuja의 블로그

본 게시물은 유자님의 아이디어를 차용한것입니다