1498-B, *1300

Problem - 1498B - Codeforces

문제

• 높이가 1이고 너비가 2의 거듭제곱 형태$(w_{i} = 2^{k})$인 블록 $n(1\leq n \leq 10^{5})$개가 주어진다
• 높이가 1이고 너비가 $w$인 박스가 있을 때, 모든 블록을 담으려면 최소 몇 개의 박스가 필요한가?
  (단, $w \geq \mathrm{max(w_{i})}$

 

풀이1

Greedy
너비가 큰 블록부터 상자에 넣는다.
블록이 들어간 상자들 중 남는 자리가 있으면 그 곳에 채워넣고, 없으면 새로운 상자에 블록을 넣는다

 

Claim 1
$w_{i}$가 2의 거듭제곱 꼴이고 $w_{1}$ 부터 $w_{n}$이 증가할때
$$\begin{aligned}
&w_{1}+w_{2}+\cdot \cdot \cdot+ w_{n}>w_{0},\ w_{1} \leq w_{0}\\
&\Rightarrow \exists \ i\in [1,\ n) \text{ s.t. } w_{1}+w_{2}+\cdot \cdot \cdot+ w_{i}=w_{0}
\end{aligned}
$$

$\because$
$w_{1}+w_{2}+\cdot \cdot \cdot+ w_{n}>2,\ w_{1} \leq 2$에 대해
$w_{1}=2$이면 $i = 1$ 에서 준 명제가 성립한다
$w_{1}<2$이면 $w_{1}+w_{2}+\cdot \cdot \cdot+ w_{n}=(1+1)+1+\cdot \cdot \cdot + 1$ 이므로 성립한다

$w_{0}=2^{k}(k \geq 1)$일 때 준 명제가 성립한다고 가정하자. 그러면
$w_{1}+w_{2}+\cdot \cdot \cdot+ w_{n}>2^{k+1},\ w_{1} \leq 2^{k+1}$에 대해
i) $w_{1}=2^{k+1}$이면 $i=1$에서 준 명제가 성립하고
ii) $w_{1}<2^{k+1} \text{ i.e. } w_{i}\leq 2^{k}$일 때 
$w_{1}+w_{2}+\cdot \cdot \cdot+ w_{j} = 2^{k}$($\because$ 가정)
$w_{i+1}+w_{2}+\cdot \cdot \cdot+ w_{k} = 2^{k},\ k < n$($\because$ 가정)
따라서 $i = k$에서 준 명제가 성립한다

수학적 귀납법에 의해 준 명제는 성립한다□

 

Claim 2
최적 알고리즘을 사용하여 상자에 넣은 블록들의 자리를
사용한 상자의 높이 변화 없이 서로 바꿔서 greedy 알고리즘 결과와 같게 만들 수 있다

$pf$
최적 알고리즘의 각 상자를 내림차순으로 정렬하자
또한 편의상 greedy 알고리즘에서 상자에 블록을 넣을 때 항상 왼쪽부터 채워 넣는다고 하자. 그러면
최적 알고리즘과 greedy 알고리즘 모두 각 층마다 왼쪽 블록이 오른쪽 블록보다 크거나 같은 상태이다

두 알고리즘의 해를 동시에 아래부터 위쪽으로, 왼쪽부터 오른쪽으로 살펴보자
처음으로 나오는 다른 크기의 블록을 $B_{o},\ B_{g}$ 이라고 하면

i) $B_{o} < B_{g}$

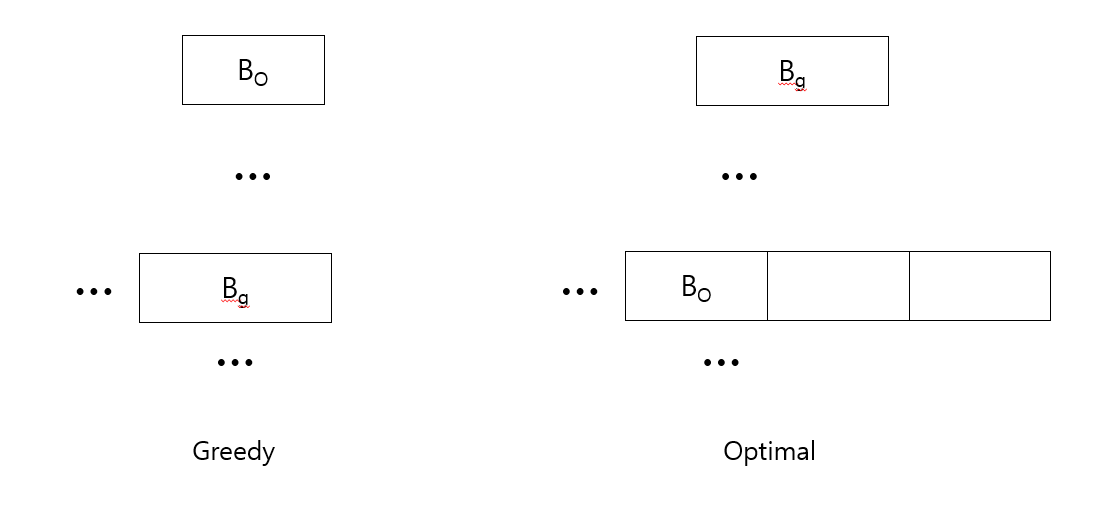
$B_{o}$를 포함한 오른쪽에 있는(물론 없을수도 있다) 모든 블록의 너비합은
가. $B_{g}$의 너비보다 크다
- Claim 1 에 의해 앞부분 일부의 너비합은 $B_{g}$와 같다. 이 부분을 위쪽에 있는 $B_{g}$와 바꾼다
나. $B_{g}$의 너비보다 작거나 같다
- 전부 위쪽에 있는 $B_{g}$와 바꾼다

ii) $B_{o} > B_{g}$
이런 경우는 존재하지 않는다.
$B_{o}$가 더 크다면 greedy 알고리즘에서 $B_{g}$보다 $B_{o}$를 먼저 배정한다
따라서 $B_{o}$를 배정할 때에는 $B_{g}$ 자리는 비어있거나 $B_{o}$ 보다 큰 블록이 차지하고 있어야한다□

priority queue, $O(nlog\ n)$

#include <bits/stdc++.h>
#define endl "\n"
#define loop(i, n) for(int i = 1; i <= n; i++)
using namespace std;
 
int n, w;
priority_queue<int, vector<int>, less<int> > pq;
 
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
 
    int t;
    cin >> t;
    while(t--){
        cin >> n >> w;
        int tmp;
        loop(i, n) {
            cin >> tmp;
            pq.push(tmp);
        }
 
        priority_queue<int, vector<int>, less<int> > basket;
        basket.push(w);
        while(!pq.empty()){
            int b = pq.top(); pq.pop();
            int remain = basket.top(); basket.pop();
            if(remain >= b) basket.push(remain-b);
            else{
                basket.push(remain);
                basket.push(w-b);
            }
        }
        cout << basket.size() << endl;
    }
 
    return 0;
}cs

 

풀이2

Greedy
상자에 가장 큰 블록을 넣는다
남은 공간에 들어갈 수 있는 가장 큰 블록을 찾아 넣는다. 없으면 새로운 상자에 그 블록을 넣는다(반복)

 

Claim 3
최적 알고리즘을 사용하여 상자에 넣은 블록들의 자리를
사용한 상자의 높이 변화 없이 서로 바꿔서 greedy 알고리즘 결과와 같게 만들 수 있다

$pf$
최적 알고리즘의 각 상자를 내림차순으로 정렬하자
또한 편의상 greedy 알고리즘에서 상자에 블록을 넣을 때 항상 왼쪽부터 채워 넣는다고 하자. 그러면
최적 알고리즘과 greedy 알고리즘 모두 각 층마다 왼쪽 블록이 오른쪽 블록보다 크거나 같은 상태이다

두 알고리즘의 해를 동시에 아래부터 위쪽으로, 왼쪽부터 오른쪽으로 살펴보자
처음으로 나오는 다른 크기의 블록을 $B_{o},\ B_{g}$ 이라고 하면

i) $B_{o} < B_{g}$

$B_{o}$를 포함한 오른쪽에 있는(물론 없을수도 있다) 모든 블록의 너비합은
가. $B_{g}$의 너비보다 크다
- Claim 1 에 의해 앞부분 일부의 너비합은 $B_{g}$와 같다. 이 부분을 위쪽에 있는 $B_{g}$와 바꾼다
나. $B_{g}$의 너비보다 작거나 같다
- 전부 위쪽에 있는 $B_{g}$와 바꾼다

ii) $B_{o} > B_{g}$
이런 경우는 존재하지 않는다
greedy 알고리즘에서 $B_{g}$를 배열할 시점에 $B_{o}$ 블록도 아직 배정하지 않은 상태이다
greedy 알고리즘은 큰 블록을 우선으로 배정하므로
$B_{o}$가 더 큰 블록이었다면 $B_{o}$을 배정했을 것이다□

bitmasks, $O(nlog\ \mathrm{w_{max}})$

#include <bits/stdc++.h>
#define endl "\n"
#define loop(i, n) for(int i = 1; i <= n; i++)
using namespace std;
 
int n, w;
 
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
 
    int t;
    cin >> t;
    while(t--){
        cin >> n >> w;
        vector<int> cnt(20);
        int tmp;
        loop(i, n){
            cin >> tmp;
            cnt[log2(tmp)]++;
        }
 
        int res = 1, remain = w;
        loop(i, n){
            int largest = -1;
 
            for(int size = 19; size >= 0; size--){
                if(cnt[size] && (1 << size) <= remain) {
                    largest = size;
                    break;
                }
            }
 
            if(largest == -1){
                res++;
                remain = w;
                for(int size = 19; size >= 0; size--){
                    if(cnt[size] && (1 << size) <= remain) {
                        largest = size;
                        break;
                    }
                }
            }
 
            cnt[largest]--;
            remain -= 1 << largest;
        }
 
        cout << res << endl;
 
    }
 
    return 0;
}cs

multiset, $O(nlog\ n)$

#include <bits/stdc++.h>
#define endl "\n"
#define loop(i, n) for(int i = 1; i <= n; i++)
using namespace std;
 
int n, w;
 
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
 
    int t;
    cin >> t;
    while(t--){
        cin >> n >> w;
        multiset<int> ms;
        int tmp;
        loop(i, n){
            cin >> tmp;
            ms.insert(tmp);
        }
 
        int res = 1, remain = w;
        while(!ms.empty()){
            auto it = ms.upper_bound(remain);
            if(it != ms.begin()){
                it--;
                remain -= *it;
                ms.erase(it);
            }
            else{
                res++;
                remain = w;
            }
        }
 
        cout << res << endl;
 
    }
 
    return 0;
}cs

풀이3

상자의 개수 $cnt$가 주어졌을 때 모든 블록을 넣을 수 있는지 검사할 수 있다면
이진탐색을 통해 $cnt$의 값을 구해낼 수 있다

먼저, 동일한 크기의 블록만을 상자에 넣는 경우를 생각하자
블록의 크기가 $4$일때 하나의 상자에는 최대 $\left \lfloor \frac{w}{4} \right \rfloor$개 들어가므로
상자의 개수가 $cnt$개이면 최대 수용할 수 있는 블록의 개수는
$$suff_{4} = cnt\left \lfloor \frac{w}{4} \right \rfloor$$

따라서 크기가 $4$인 블록의 개수가 $suff_{4}$보다 크면 $cnt$를 늘려야 한다

한편, 크기가 $4$인 블록을 모두 넣을 수 있을때 크기가 $2$인 블록까지 추가하여 넣을 수 있는지 살펴보자
크기가 $4$인 블록은 크기가 $2$인 블록 두개를 붙여놓은 것으로 생각한다
그러면
$$suff_{2} = cnt\left \lfloor \frac{w}{2} \right \rfloor$$

따라서 2$\times$($4$개수)+($2$개수)가 $suff_{2}$보다 작으면 크기가 $4$인 블록과 $2$인 블록 모두를 상자에 담을 수 있다

※ 크기가 $4$인 블록이 들어가는지 반드시 먼저 확인해야 한다.
이는 크기가 $4$인 블록이 짤리지 않았음을 보장해준다
($4$블록은 다 들어가므로 그대로 두고 $2$를 채워 넣는다고 생각)

binary search, $O(n+log\ \mathrm{w_{max}}\cdot log\ n)$

#include <bits/stdc++.h>
#define endl "\n"
#define loop(i, n) for(int i = 1; i <= n; i++)
using namespace std;
 
array<int, 20> arr;
int n, w;
 
bool valid(int cnt)
{
    for(int i = 19; i >= 0; i--){
        long long suff = 1LL*cnt*(w/(1 << i));
        if(arr[i] > suff) return false;
    }
    return true;
}
 
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
 
    int t;
    cin >> t;
    while(t--){
        cin >> n >> w;
 
        for(int i = 0; i < 20; i++) arr[i] = 0;
 
        int tmp;
        loop(i, n){
            cin >> tmp;
            arr[log2(tmp)]++;
        }
 
        for(int i = 18; i >= 0; i--) arr[i] += 2*arr[i+1];
 
        int lo = 1, hi = n;
        int ans = -1;
        while(lo <= hi){
            int mid = (lo + hi) / 2;
            if(valid(mid)){
                hi = mid - 1;
                ans = mid;
            }
            else lo = mid + 1;
        }
 
        cout << ans << endl;
 
    }
 
    return 0;
}cs