-
1295-D, *1800코드포스 2021. 11. 10. 16:42
Problem - D - Codeforces
codeforces.com
문제
- 자연수 $a,\ m$이 주어질 때 $(a,m)=(a+x,m)$인 $x(0\leq x < m)$의 개수를 구하라
풀이
let
d = (a, m),
a = a'd
m = m'd
then,
(a, m) = (a+x, m)
d = (da'+x, dm') ... !division algorithm 에 의해
x = dq + r, 0 ≤ r < d
인 정수 q, r 이 유일하게 존재한다
만약 r ≠ 0 이면
d $\nmid$ (da'+r)
이므로 모순이다(두 정수 a, b의 최대공약수는 a, b 를 모두 나눈다)
따라서 x = dq 꼴이고 0 ≤ x < m 이므로 q = 0, 1, 2, ... , m'-1! 을 좀더 정리하면
d = (da'+dq, dm') = d(a'+q, m')Eu
1 = (a'+q, m')이때 (a'+q) 가 법 m' 에 관한 완전잉여계이므로
1 = (a'+q, m') 을 만족하는 (a'+q)의 개수는 Φ(m')이다 (Φ denotes Eular's totient function)
즉, 구하려는 값은 Φ(m')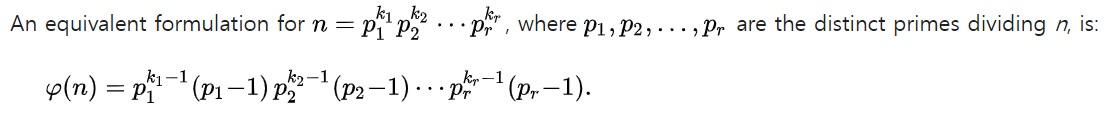
이 사실을 이용한다
m' 이 1~$10^{5}$ 범위의 소수로 나눠떨어지지 않으면 m' 은 소수이다
따라서 먼저 에라토스 테네스의 쳉를 이용하여 이 범위의 소수를 구한다그리고 구한 소수들로 m'을 소인수분해한다
※ √m' 이하의 소수들로 m' 을 계속 나눴음에도 m'이 1 보다 큰 수가 남으면 그때 남은수는 소수이다
ex)
648 = 2 x 2 x 3 x 59
√648 = 25.45.... 이하의 소수들로 648 를 계속 나누면 1보다 큰 59 가 남는데 59 는 소수이다
(∵ 59 는 √59 이하의 소수들로 나눴을 때 나눠떨어지지 않았으므로 소수이다)123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960#include <bits/stdc++.h>#define endl "\n"#define ooop(i, n) for(int i = 0; i < n; i++)#define loop(i, n) for(int i = 1; i <= n; i++)#define all(v) (v).begin(), (v).end()using namespace std;typedef long long ll;typedef pair<int, int> pi;typedef pair<ll, ll> pl;bool seive[1000001] {};void find_prime(){seive[2] = true;for(int i = 3; i < size(seive); i += 2) seive[i] = true;for(int i = 3; i*i < size(seive); i += 2){if(seive[i]){for(int j = i*i; j < size(seive); j += i) seive[j] = false;}}}int main(){ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);int t;cin >> t;find_prime();vector<ll> prime;loop(i, size(seive)){if(seive[i]) prime.emplace_back(i);}while(t--){ll a, m;cin >> a >> m;ll d = gcd(a, m);ll m_prime = m/d;ll res = 1;bool is_prime = true;for(const auto p: prime){if(m_prime%p == 0){is_prime = false;int exp = 0;while(m_prime%p == 0){exp++;m_prime /= p;}res *= (p-1)*pow(p, exp-1);}}if(m_prime > 1) res *= m_prime-1;cout << (is_prime? m_prime-1: res) << endl;}return 0;}cs'코드포스' 카테고리의 다른 글
1301-C, *1700 (0) 2021.12.24 1301-D, *2000 (0) 2021.12.24 1295-C, *1600 (0) 2021.11.10 1295-B, *1700 (0) 2021.11.10 1284-C, *1600 (0) 2021.11.03